Relácia kolmosti
Použitím zhodnosti úsečiek a uhlov budeme teraz definovať ďalšie geometrické pojmy: pravý uhol, kolmosť priamok a rovín. Pod pojmom relácia budeme rozumieť vzťah medzi dvoma geometrickými objektami.
 
 
Step: Pravý uhol ...
  Pravý uhol
Uhol, ktorý je zhodný s uhlom k nemu vedľajším, nazývame pravý uhol.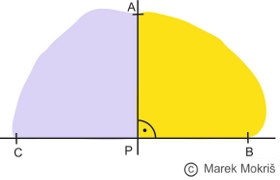

Príklad:
Uhol APB je zhodný s uhlom CPA, ktorý je k nemu vedľajší. Preto uhol APB je pravý uhol (viď obrázok).
 
 
Step: Kolmé priamky ...
  Kolmé priamky

Dve rôznobežné priamky AP, BP nazývame kolmé práve vtedy, keď uhol APB je pravý.
Označenie dvojice kolmých priamok: .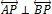

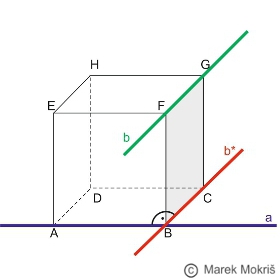
Dve mimobežné priamky a, b sú kolmé práve vtedy, keď existuje taká priamka b*, b∥b*, že priamky a*,b sú kolmé rôznobežky.

Príklad:
Nech je daná kocka ABCDEFGH, priamku AB označíme a, priamku FG označíme b, priamku BC označíme b* (viď obrázok).
  • Priamky AB, BC sú navzájom kolmé, pretože uhol ABC je pravý.
  • Priamky a, b sú kolmé mimobežky, pretože existuje taká priamka b*, b∥b* a súčasne a⊥b*.
 
 
Step: Priamka kolmá na rovinu ...
  Priamka kolmá na rovinu
Priamka p a rovina α sú navzájom kolmé, ak priamka p je kolmá na každú priamku roviny α.
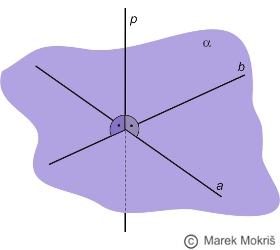
Označenie: p⊥α.

Kritérium kolmosti priamky a roviny:
Ak je priamka p kolmá na dve rôznobežné priamky a, b roviny α, potom je kolmá na rovinu α.
 
 
Step: Kolmé roviny ...
  Kolmé roviny
Definícia a kritérium kolmosti dvoch rovín:
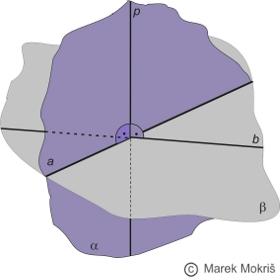
Rovina α je kolmá na rovinu β, ak rovina α obsahuje priamku kolmú na β.
Označenie: α⊥β.