Pytagorova veta
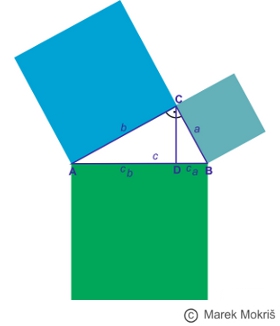
Daný je pravouhlý trojuholník ABC s pravým uhlom pri vrchole C. Výška na stranu c (úsečka CD) rozdeľuje trojuholník ABC na dva trojuholníky ADC a DBC, ktoré sú s trojuholníkom ABC podobné (podľa vety uu o podobnosti trojuholníkov). Úsečku AD označíme c
b
, úsečku DB označíme c
a
. Skúmajme, čomu sa rovná a
2
+b
2
.
Na základe Euklidových viet o odvesne platí:


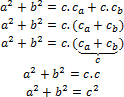
Zo vzťahu a 2 +b 2 = c 2 vyplýva, že obsah štvorca nad preponou sa rovná súčtu obsahov štvorcov nad oboma odvesnami.
Na základe Euklidových viet o odvesne platí:


Zo vzťahu a 2 +b 2 = c 2 vyplýva, že obsah štvorca nad preponou sa rovná súčtu obsahov štvorcov nad oboma odvesnami.
|
Pytagorova veta:
Ak trojuholník ABC je pravouhlý s pravým uhlom pri vrchole C, potom platí a 2 +b 2 = c 2 , kde a, b, c sú dĺžky strán trojuholníka ABC. Obrátená Pytagorova veta: Ak v trojuholníku ABC platí a 2 +b 2 = c 2 , potom trojuholník ABC je pravouhlý s pravým uhlom pri vrchole C. |