Obsah jednoduchých rovinných útvarov
V tejto časti odovdíme vzťahy pre výpočet obsahu jednoduchých rovinných útvarov.
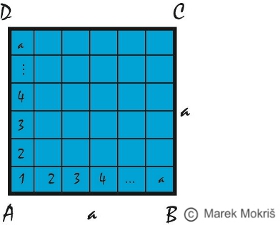
Pri určení obsahu štvorca je potrebné zistiť, koľko jednotkových štvorcov je možné umiestniť do štvorca ABCD. Tento počet je a.a (pozri obrázok).
Vzorec pre výpočet obsahu štvorca je S = a 2 , kde a je veľkosť strany štvorca.
Vzorec pre výpočet obsahu štvorca je S = a 2 , kde a je veľkosť strany štvorca.
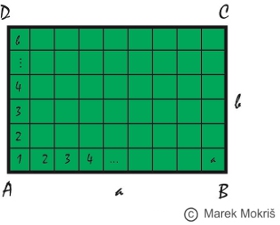
Pri určení obsahu obdĺžnika je potrebné zistiť, koľko jednotkových štvorcov je možné umiestniť do obdĺžnika ABCD. Tento počet je a.b (pozri obrázok).
Vzorec pre výpočet obsahu obdĺžnika je S = a.b , kde a, b sú veľkosti strán obdĺžnika.
Vzorec pre výpočet obsahu obdĺžnika je S = a.b , kde a, b sú veľkosti strán obdĺžnika.
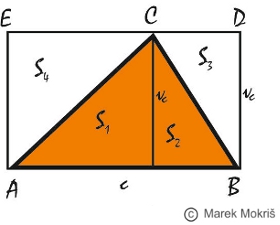
Pri odvodení vzťahu pre obsah trojuholníka, opíšeme trojuholníku ABC obdĺžnik ABDE (pozri obrázok). Ten je rozdelený na štyri trojuholníky s obsahmi S1, S2, S3, S4. Na základe zhodnosti trojuholníkov, pre ich obsahy platí S1 = S4 a S2 = S3.
Potom obsah trojuholníka ABC je polovicou obsahu
obdĺžnika ABDE.
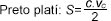
Potom obsah trojuholníka ABC je polovicou obsahu
obdĺžnika ABDE.
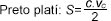
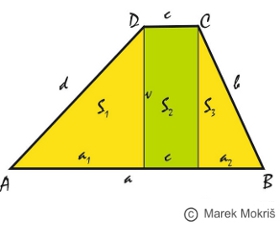
Lichobežník ABCD sme rozdelili na dva trojuholníky s obsahmi
(S 1 , S 3 ) a jeden obdĺžnik s obsahom S 2 .

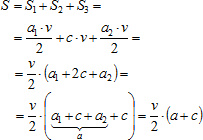
(S 1 , S 3 ) a jeden obdĺžnik s obsahom S 2 .

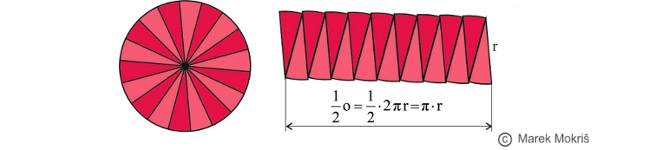
Kruh rozdelíme na rovnaké kruhové výseky, ktoré potom poukladáme vedľa seba (pozri obrázok). Pri nekonečnom stenčovaní kruhového výseku by naukladané kruhové výseky tvorili obdĺžnik so stranami a = π.r, b = r.
Potom obsah kruhu určíme S = π.r.r = π.r 2 , kde r je veľkosť polomeru kruhu.
Potom obsah kruhu určíme S = π.r.r = π.r 2 , kde r je veľkosť polomeru kruhu.