Zhodnosť uhlov
V tejto časti zavedieme pojem zhodnosť uhlov. Budeme charakterizovať grafické porovnávanie dvoch uhlov. Zadefinujeme grafický súčet a rozdiel dvoch uhlov.
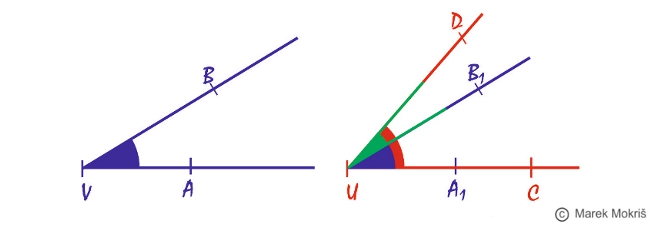
Konvexný uhol AVB je zhodný s konvexným uhlom CUD práve vtedy, keď na polpriamkach UC, UD existujú také body A
1
, B
1
, že platí
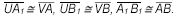
Zápis: ∢AVB ≅ ∢CUD.
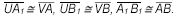
Zápis: ∢AVB ≅ ∢CUD.
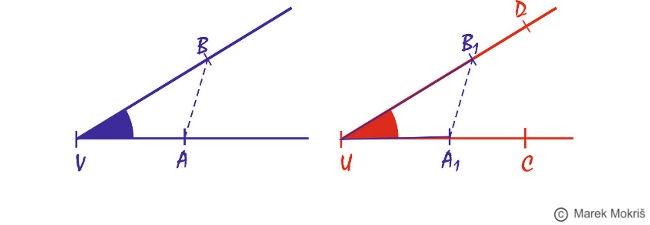
Porovnávanie uhlov
Pri grafickom porovnávaní uhlov využívame prenášanie uhlov. Konštrukčný postup:
Pri grafickom porovnávaní uhlov využívame prenášanie uhlov. Konštrukčný postup:
|
|||||||||||||||
|
|||||||||||||||
|
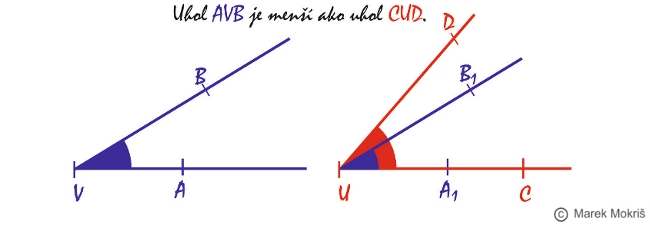
Grafický súčet uhlov
Pri konštrukcii grafického súčtu dvoch uhlov budeme tiež využívať prenášanie uhla. Konštrukčný postup:
Pri konštrukcii grafického súčtu dvoch uhlov budeme tiež využívať prenášanie uhla. Konštrukčný postup:
|
|||
|
|||
|
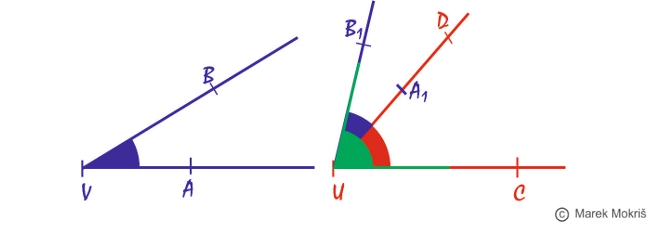
Grafický rozdiel uhlov
Pri konštrukcii grafického rozdielu dvoch uhlov budeme tiež využívať prenášanie uhlov. Konštrukčný postup:
Pri konštrukcii grafického rozdielu dvoch uhlov budeme tiež využívať prenášanie uhlov. Konštrukčný postup:
|
|||
|
|||
|